Формула с золотым сечением и ее применение
17 февраля, 2017 в 14:52,
Нет комментариев
При создании полевой теории гравитации было получено уравнение (http://gravitus.ucoz.ru/blog/formula_s_zolotym_secheniem_i_ee_primenenie/2017-02-17-9) p^6+4p^4-8=0
где p – производная.
Это уравнение имеет шесть решений:
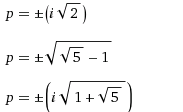
где i — мнимая единица.
Как известно, производная в своей онтологии – это тангенс угла наклона касательной, т.е. прямой линии. Используя этот факт, а также особенности преобразований, была получена формула квантования кривых внутри данного семейства:
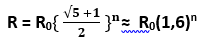
где: n =0,1,2,3… - целочисленный показатель степени
(√5 +1)/2 = 1,61803398875....≈ 1.6 - число "золотого сечения"
R0 - начальный параметр
Только здесь существует одно «но»: формула выводится при условии, что мнимые корни используются совместно с действительными, как будто они тоже являются действительными. Вначале проверим, насколько пригодна данная формула для астрономических расчетов, а затем обратимся к онтологии комплексных чисел с тем, чтобы проверить ее полноту.
1) При R0, равному радиусу Земли, при различных значениях n имеем границы радиационных поясов Земли и зону расположения Луны.
В настоящее время обнаружены три радиационных пояса. Они расположены между широтами α=±300. Опять фиксируем этот угол.
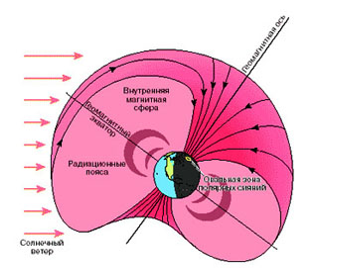
Внутренний пояс расположен в диапазоне, определяемом значениями n=0 и n=1.
Внешний пояс – в диапазоне n=2 и n=3.
Третий пояс - в диапазоне n=4 и n=5.
Луна располагается в зоне, определяемой показателями степени n=8 и n=9.
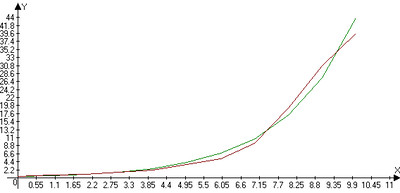
2) При R0, равному радиусу Меркурия (0.4а.е.), получаем значения орбит планет Солнечной системы (в астрономических единицах а.е.):
1) п=0 орбита Меркурия
2) п=1 - 0.6а.е. - Венера
3) п=2 - 1а.е – Земля
4) п=3 - 1.6а.е - Марс
5) п=4 - 2.6а.е. - астероиды (начало)
6) п=5 - 4.2а.е. - астероиды (конец)
7) п=6 - 6.7а.е. - Юпитер
8) п=7 - 10.7а.е. - Сатурн
9) п=8 - 17.1а.е. - Уран
10) п=9 - 27.4а.е. - Нептун
11)п=10 - 43.8а.е. – Плутон
По результатам расчетов строим график (зеленый) и сравниваем с табличными данными (красный).
3) При R0, равному радиусу Меркурия (R0=2,4 тыс. км), получаем радиусы планет Солнечной системы:
• n=0
R равен радиусу Меркурия 2,4 тыс. км.
• n=1 R=3.9 тыс. км.
Радиус Марса (табличное значение) равен 3,4 тыс. км.
• n=2 R=6.2 тыс. км.
Радиус Венеры равен 6,1 тыс. км.
Радиус Земли равен 6,4 тыс. км.
Получаем: 6,1 тыс. км - 6.2 тыс. км - 6,4 тыс. км
• n=5 R=25,6 тыс. км.
Радиус Нептуна равен 24,8 тыс. км.
Радиус Урана равен 26,2 тыс. км.
Получаем: 24,8 тыс. км - 25,6 тыс. км - 26,2 тыс. км
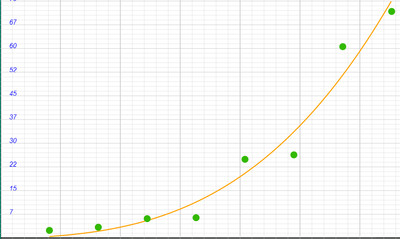
• n=7 R=65,5 тыс. км.
Радиус Сатурна равен 60,3 тыс. км
Радиус Юпитера равен 71,4 тыс. км.
Получаем: 60,3 тыс. км - 65,5 тыс. км - 71,4 тыс. км
Строим график возрастания радиусов планет в зависимости от численных значений:
4) Рассчитаем отношение орбит планет (большая полуось, обозначим R) к радиусам непосредственно самих планет (обозначим r и используем общедоступные табличные данные).
Меркурий: 57.9млн.км/2.4тыс.км=24.1х10^3
Везде будет коэффициент 10^3, поэтому обойдемся без него.
Итак, расчеты:
Меркурий - 24.1
Венера - 17.7
Земля - 23.4
Марс - 67.0
Юпитер - 10.9
Сатурн - 23.7
Уран - 109.6
Нептун - 181.4
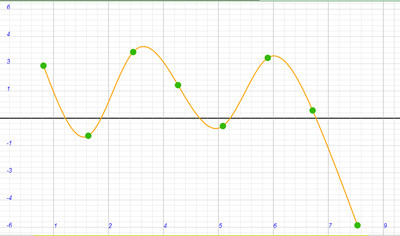
Теперь возведем число (1.6) в степень n, где n=0,1,2,3...
Получаем:
(1.6)^5=10.5
(1.6)^6=16.8
(1.6)^7=26.8
(1.6)^8=43.0
(1.6)^9=68.7
(1.6)^10=110.0
(1.6)^11=175.9
Строим график, по оси X которого будем откладывать номер планеты (для Меркурия N=1 и далее), а по оси Y - разность между фактическими значениями отношений для планет от значений числа 1.6 в степени n. Получаем периодическую кривую:
5) Рассчитаем радиусы орбит спутников Марса: Фобоса и Деймоса.
В пункте 3 мы получили значение радиуса R=3.9 тыс. км. Используя данное значение, как начальный параметр R0, при n=2 и n=4 получаем соответственно:
• радиус орбиты Фобоса 10,0 тыс. км.
• радиус орбиты Деймоса 25,6 тыс. км
Табличные данные орбит этих спутников таковы:
• радиус орбиты Фобоса 9,4 тыс. км.
• радиус орбиты Деймоса 23,5 тыс. км.
Теперь в формулу подставим табличное значение радиуса Марса R0=3,4 тыс. км.
Соответственно, при n=2 и n=4 получаем:
• радиус орбиты Фобоса 8,7 тыс. км.
• радиус орбиты Деймоса 22,3 тыс. км.
Подведем итог: во всех рассмотренных случаях наблюдается локализация табличных значений вокруг значений, рассчитанных по формуле с золотым сечением. Формула работает приблизительно, но не точно. Явно ощущается ее неполнота. Это связано с тем, что при ее выводе вообще не использованы особенности комплексных чисел,
рассмотренных в публикации "Наблюдатель и мнимое пространство".