Гравитация и квантовая механика в макромире

Квантовая механика "работает" не только в микромире. На видео предоставлено доказательство того, что она "работает" и в макромире. Элементарно простой анализ Закона Всемирного тяготения в рамках третьего закона Кеплера показывает, что в теории гравитации не учтена периодическая функция, которая явно там должна присутствовать. Это видно из графика, построенного по результатам расчетов. 

Формула с золотым сечением и ее применение

При создании полевой теории гравитации было получено уравнение (http://gravitus.ucoz.ru/blog/formula_s_zolotym_secheniem_i_ee_primenenie/2017-02-17-9) 

p^⁶+4p^⁴-8=0 

где p – производная. 

Это уравнение имеет шесть решений: 

 

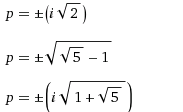
где i — мнимая единица. 

Как известно, производная в своей онтологии – это тангенс угла наклона касательной, т.е. прямой линии. Используя этот факт, а также особенности преобразований, была получена формула квантования кривых внутри данного семейства: 

 

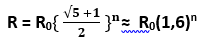
где: n =0,1,2,3… - целочисленный показатель степени 
(√5 +1)/2 = 1,61803398875....≈ 1.6 - число "золотого сечения" 
R₀ - начальный параметр 

Только здесь существует одно «но»: формула выводится при условии, что мнимые корни используются совместно с действительными, как будто они тоже являются действительными. Вначале проверим, насколько пригодна данная формула для астрономических расчетов, а затем обратимся к онтологии комплексных чисел с тем, чтобы проверить ее полноту. 

1) При R₀, равному радиусу Земли, при различных значениях n имеем границы радиационных поясов Земли и зону расположения Луны. 

В настоящее время обнаружены три радиационных пояса. Они расположены между широтами α=±300. Опять фиксируем этот угол. 

 

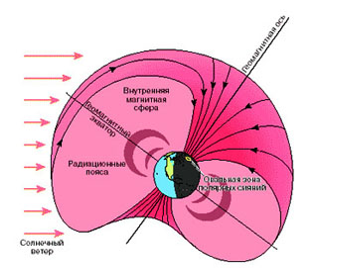
Внутренний пояс расположен в диапазоне, определяемом значениями n=0 и n=1. 
Внешний пояс – в диапазоне n=2 и n=3. 
Третий пояс - в диапазоне n=4 и n=5. 
Луна располагается в зоне, определяемой показателями степени n=8 и n=9. 

2) При R₀, равному радиусу Меркурия (0.4а.е.), получаем значения орбит планет Солнечной системы (в астрономических единицах а.е.): 

1) п=0 орбита Меркурия 
2) п=1 - 0.6а.е. - Венера 
3) п=2 - 1а.е – Земля 
4) п=3 - 1.6а.е - Марс 
5) п=4 - 2.6а.е. - астероиды (начало) 
6) п=5 - 4.2а.е. - астероиды (конец) 
7) п=6 - 6.7а.е. - Юпитер 
8) п=7 - 10.7а.е. - Сатурн 
9) п=8 - 17.1а.е. - Уран 
10) п=9 - 27.4а.е. - Нептун 
11)п=10 - 43.8а.е. – Плутон 

По результатам расчетов строим график (зеленый) и сравниваем с табличными данными (красный). 

 

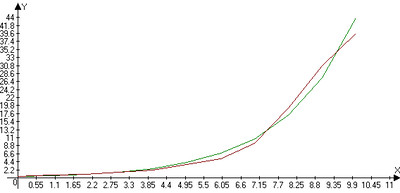
3) При R₀, равному радиусу Меркурия (R₀=2,4 тыс. км), получаем радиусы планет Солнечной системы: 

• n=0 
R равен радиусу Меркурия 2,4 тыс. км. 
• n=1 R=3.9 тыс. км. 
Радиус Марса (табличное значение) равен 3,4 тыс. км. 
• n=2 R=6.2 тыс. км. 
Радиус Венеры равен 6,1 тыс. км. 
Радиус Земли равен 6,4 тыс. км. 
Получаем: 6,1 тыс. км - 6.2 тыс. км - 6,4 тыс. км 
• n=5 R=25,6 тыс. км. 
Радиус Нептуна равен 24,8 тыс. км. 
Радиус Урана равен 26,2 тыс. км. 
Получаем: 24,8 тыс. км - 25,6 тыс. км - 26,2 тыс. км 
• n=7 R=65,5 тыс. км. 
Радиус Сатурна равен 60,3 тыс. км 
Радиус Юпитера равен 71,4 тыс. км. 
Получаем: 60,3 тыс. км - 65,5 тыс. км - 71,4 тыс. км 

Строим график возрастания радиусов планет в зависимости от численных значений: 

 

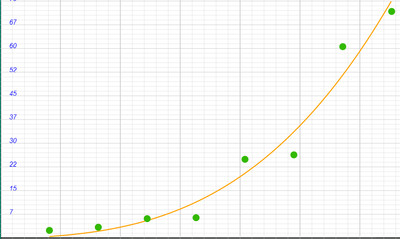
4) Рассчитаем отношение орбит планет (большая полуось, обозначим R) к радиусам непосредственно самих планет (обозначим r и используем общедоступные табличные данные). 

Меркурий: 57.9млн.км/2.4тыс.км=24.1х10^³ 
Везде будет коэффициент 10^³, поэтому обойдемся без него. 

Итак, расчеты: 
Меркурий - 24.1 
Венера - 17.7 
Земля - 23.4 
Марс - 67.0 

Юпитер - 10.9 
Сатурн - 23.7 
Уран - 109.6 
Нептун - 181.4 

Теперь возведем число (1.6) в степень n, где n=0,1,2,3... 
Получаем: 
(1.6)^⁵=10.5 
(1.6)^⁶=16.8 
(1.6)^⁷=26.8 
(1.6)^⁸=43.0 
(1.6)^⁹=68.7 
(1.6)^¹⁰=110.0 
(1.6)^¹¹=175.9 

Строим график, по оси X которого будем откладывать номер планеты (для Меркурия N=1 и далее), а по оси Y - разность между фактическими значениями отношений для планет от значений числа 1.6 в степени n. Получаем периодическую кривую: 

 

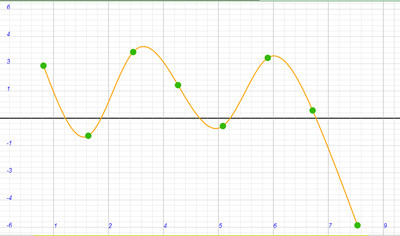
5) Рассчитаем радиусы орбит спутников Марса: Фобоса и Деймоса. 

В пункте 3 мы получили значение радиуса R=3.9 тыс. км. Используя данное значение, как начальный параметр R₀, при n=2 и n=4 получаем соответственно: 
• радиус орбиты Фобоса 10,0 тыс. км. 
• радиус орбиты Деймоса 25,6 тыс. км 

Табличные данные орбит этих спутников таковы: 
• радиус орбиты Фобоса 9,4 тыс. км. 
• радиус орбиты Деймоса 23,5 тыс. км. 

Теперь в формулу подставим табличное значение радиуса Марса R₀=3,4 тыс. км. 
Соответственно, при n=2 и n=4 получаем: 
• радиус орбиты Фобоса 8,7 тыс. км. 
• радиус орбиты Деймоса 22,3 тыс. км. 

Подведем итог: во всех рассмотренных случаях наблюдается локализация табличных значений вокруг значений, рассчитанных по формуле с золотым сечением. Формула работает приблизительно, но не точно. Явно ощущается ее неполнота. Это связано с тем, что при ее выводе вообще не использованы особенности комплексных чисел, 

Электромагнитная теория гравитации

Электромагнитная  теория гравитации стартует из одного из фундаментальных законов сохранения и, в итоге, не выходя за рамки классической физики, выводится волновое уравнение.        В полученном волновом уравнении, в отличие от общепринятых волновых уравнений, применяемых в современной физике, присутствует некая функция, которая объясняет смысл квантовой механики, принцип неопределенности Гейзенберга и т.д., возвращая многие физические проблемы в лоно классической физике. Кроме того, было получено, что эффект притяжения периферийного тела к центральному формируют силы электромагнитной природы с конкретным видом электрической и магнитной составляющих. Также из анализа полученных результатов следует, что электромагнитное поле является переменным, причем электрическая и магнитная составляющие центрального тела колеблются по определенным законам, которые можно графически визуализировать.

      В качестве доказательства вышеизложенного приведем два примера.

 

1. Построение графика для планет Солнечной системы с ярко выраженными квантово-механическими  атрибутами.

 

      Третий закон Кеплера: квадраты периодов Т обращения планет вокруг центрального тела пропорциональны кубам больших полуосей а их орбит:

 

Т²=4 π² а³ /(GM)                        (1.1.2)

 

Представим  (1.1.2) в виде:

а = (GM/4π²)^1/3 (Т²)^1/3                 (1.1.3)

 

               где: G - постоянная гравитации

                      М - масса центрального тела

 

Теперь произведем обозначения:

λ_i =(GM/4π²)^1/3 = const                (1.1.4)

 

     K_ij  = (T²_ij)^1/3                          (1.1.5)

 

где: i – индекс планетной системы

       j - индекс планеты (спутника)

      λ_i - константа для  i-ой планетной системы.

 

Тогда (1.1.3) можно переписать в виде:

 

                                  а_ij=λ_iK_ij                                  (1.1.6)

 

Формула (1.1.2) достаточно хорошо согласуется с астрономическими наблюдениями.

 

Однако имеются примеры, не подающиеся никакому объяснению. Так, например, спутник Мимас в планетной системе Сатурна имеет параметры (см. Э.В. Кононович, В.И. Мороз – Общий курс астрономии: Учебное пособие / под. Ред. В.В. Иванова Изд. 2-е, испр. М.: Едиториал УРСС 2004. – стр. 503 (приложение)):

 

а=158,5 тыс. км

Т=1,370 суток

 

Однако, при таком значении а период Т должен быть, согласно (1.1.2), совсем другим: Т=0,75 суток. Это подтверждается даже тем фактом, что у соседних спутников параметры соответствуют (1.1.2).

 

Так, у спутника Янус:

а=151,5 тыс. км

Т=0,69 суток

 

А у спутника Энцелад:

а=238,0 тыс. км

Т=0,942 суток

 

Приведенный пример дает нам полное право усомниться в формуле (1.1.2) и провести ряд исследований на возможность описания параметров планет (спутников) другими законами.

 

По формуле (1.1.4) для Солнечной системы вычислим значение  λ ₀ в единицах суток и миллионов километров:

                                          λ_0 =2.933 млн. км/ (сут) ^2/3

 

и для простоты опустим в дальнейшем размерность  λ ₀  и К₀j  (будем считать их безразмерными). По формуле (1.1.5) рассчитаем   К₀j  и (K_0j)^1/2 для всех планет Солнечной системы (Таблица 1.1.1). Кроме того, введем целые числа N_0j, равные приближенным до целого числа значениям :

 

N_oj =   [√K_oj]                               (1.1.7)

 

Таблица 1.1.1

i	Планета	Период Toj	Koj	√Koj	Noj
1	Меркурий	87,969	19,780	4,447	4
2	Венера	224,700	36,960	6,079	6
3	Земля	365,257	51,097	7,148	7
4	Марс	686,980	77,857	8,824	9
5	Юпитер	4332,71	265,77	16,30	16
6	Сатурн	10759,50	487,37	22,08	22
7	Уран	30685	980,13	31,31	31
8	Нептун	60190	1535,85	39,19	39
9	Плутон	90800	2020,18	44,95	45

 

Числа N_0j мы вводим для того, чтобы произвести анализ третьего закона Кеплера на возможность зависимости орбит планет от каких-либо целочисленных комбинаций. Как известно, в 1885 году И. Бальмер установил, что длины волн известных в то время линий спектра водорода зависят от квадрата целых чисел, что и сыграло в дальнейшем большую роль в создании теории атома. Поэтому, если мы обнаружим какую-либо целочисленную зависимость, то это нам подскажет, каким образом строить теорию гравитации.

Введем величину:

δ_0j = (а_0j/λ₀) - N_0j²

 

и, на основании результатов Таблицы 1.1.2, построим график зависимости

δ_oj= f(N_0j), изображенный на Рис.1.1.1  (масштаб  ∆δ_oj равен масштабу ∆N_oj).

 

Таблица 1.1.2

	Планета	aoj , млн. км	aoj/λo	δoj
	Меркурий	57.909	19.744	3.744
	Венера	108.209	36.894	0.894
	Земля	149.598	51.005	2.005
	Марс	227.937	77.715	-3.285
	Юпитер	778.412	265.398	9.398
	Сатурн	1426.726	486.439	2.439
	Уран	2871.974	979.133	18.193
	Нептун	4498.257	1533.671	12.671
	Плутон	5906.361	2013.761	-11.239

 

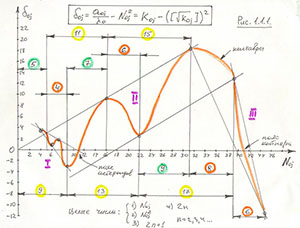
Рис.1.1.1

 

Получен очень важный результат в том плане, что он подрывает мистификацию микромира с его квантово-механическим способом описания. Квантовая механика "проникла" и в макро-мир. Она, наряду с ньютоновской механикой, описывает параметры орбит планет Солнечной системы. Это значит, что и в микро-мире, равно, как и в макро-мире, где теперь, наряду с механикой Ньютона, работает и квантовая механика, должна также работать и ньютоновская механика. Обе механики - и квантовая, и ньютоновская - дополняют друг друга, но никак не противопоставляются.

 

2. По ходу решения задачи аналитическим образом была получена формула, применение которой универсально во многих астрономических расчетах (формула приведена в приближенном виде):

 

               R = R₀{(√5 +1)/2}ⁿ ≈  R₀(1,6)ⁿ

               где: n =0,1,2,3… - целочисленный показатель степени.

               (√5 +1)/2 = 1,61803398875....≈ 1.618 -  так называемое "золотое сечение"                   R₀  - начальный параметр

               

                 Рассмотрим некоторые примеры ее применения.

 

     1. При R₀, равному радиусу Земли,  при различных значениях n имеем границы радиационных поясов Земли и зону расположения Луны, прекрасно согласующиеся с табличными данными.

 

1. При R₀, равному радиусу Меркурия (R₀=2,4 тыс. км), получаем радиусы планет Солнечной системы:                                                      1) n=0           R равен радиусу Меркурия 2,4 тыс. км                            2) n=1           R=3.9 тыс. км.

   Радиус Марса (табличное значение) равен 3,4 тыс. км.

           3) n=2           R=6.2 тыс. км.

   Радиус Венеры равен 6,1 тыс. км.

   Радиус Земли равен 6,4 тыс. км

           4) n=5           R=25,6 тыс. км

    Радиус Нептуна равен 24,8 тыс. км.

    Радиус Урана равен 26,2 тыс. км.

           5) n=7           R=65,5 тыс. км

     Радиус Сатурна равен 60,3 тыс. км

     Радиус Юпитера равен 71,4 тыс. км.

 

Сравнивая полученные результаты с табличными данными, видна определенная корреляция истинных величин вокруг рассчитанных. Например, радиусы Венеры и Земли расположены вокруг рассчитанного значения (при n=2) следующим образом: 6,1 тыс. км (Венера) – 6,2 тыс. км (рассчет) -6,4 тыс. км (Земля).

     Объяснение этого факта выходит за рамки настоящей работы.

 

2.3 Как продолжение пункта 2.2,  рассчитаем радиусы орбит спутников Марса: Фобоса и Деймоса. В пункте 2.2 мы получили значение радиуса R=3.9 тыс. км. Используя данное значение как радиус Марса R_0,  получаем при n=2 и n=4 соответственно:

    - радиус орбиты Фобоса 10,0 тыс. км.

    - радиус орбиты Деймоса 25,6 тыс. км.

Табличные данные орбит этих спутников таковы:

    - радиус орбиты Фобоса 9,4 тыс. км.

    - радиус орбиты Деймоса 23,5 тыс. км.

Теперь в формулу подставим табличное значение радиуса Марса R₀=3,4 тыс. км. Соответственно, при n=2 и n=4 получаем:

    - радиус орбиты Фобоса 8,7 тыс. км.

    - радиус орбиты Деймоса 22,3 тыс. км.

 

Сравнивая табличные данные с полученными при разных значениях радиуса Марса, мы видим, что табличные данные находятся «посередине» между расчетными величинами. Так же, как и в пункте 2.2, объяснение этого факта выходит за рамки настоящей работы, так как смысл подобных демонстраций – только лишь в показе зависимости параметров небесных тел от целочисленных значений переменной n  в формуле. Коротко лишь отметим, что в пункте 2.2 рассматривается система, центральным телом которым является Солнце, принадлежащее одному энергетическому масштабу, а в пункте 2.3. – другая система, где Марс принадлежит другому энергетическому масштабу.

 

2.4. При R₀, равному радиусам планет – гигантов, и при n=1 по формуле получаем границы расположения их  колец.

 

 Таким образом, приведенных примеров достаточно для того, чтобы любой человек, не имеющий специального образования, мог удостовериться в том, что целые числа (в частности, показатель степени n в вышеупомянутой формуле, числа К, N и комбинации 2n и 2n+1 на графике) свидетельствуют о квантово-механическом способе описания данного явления.

http://gravitus.ucoz.ru/news/ehlektromagnitnaja_teorija_gravitacii/2014-03-26-12

"Котлеты" и "мухи" гравитации

Как стало известно из сообщений, гравитационные волны были зарегистрированы 14 сентября 2015 года в 05:51 утра по летнему североамериканскому восточному времени (13:51 по московскому времени) на двух детекторах-близнецах лазерной интерферометрической гравитационно-волновой обсерватории LIGO, расположенных в Ливингстоне (штат Луизиана) и Хэнфорде (штат Вашингтон) в США.

Возмущения порождены парой черных дыр (в 29 и 36 раз тяжелее Солнца) в последние доли секунды перед их слиянием в более массивный вращающийся гравитационный объект (в 62 раза тяжелее Солнца). Слияние черных дыр произошло 1,3 миллиарда лет назад (столько времени гравитационное возмущение распространялось до Земли).

Сообщение о регистрации гравитационных волн вызвало в мире не однозначную реакцию: не только эйфорию по поводу подтверждения предсказаний ОТО, но и волну жесткой критики эксперимента.

Приведем выдержку из статьи академика РАН, научного руководителя НТЦ УП РАН Владислава Ивановича Пустовойта.
Что такое гравитационная волна? Во-первых, начнем с того, что в 1916 году Альбертом Эйнштейном были сформулированы уравнения, которые многие знают.

Главная идея этих уравнений состоит в том, что он пытался описать, как устроен мир. И пришел к выводу – я не буду подробно говорить, это
другая тема – что нужно написать некие уравнения, где R – это тензор
кривизны пространства и времени, четырехмерное пространство. Метрика
пространства определяется материей или, точнее, тензорами энергии
импульсов в правой части этих уравнений. Некая G – это константа, C –
скорость света. Вот основные уравнения общей теории относительности.
http://www.pravmir.ru/chto-takoe-gravitatsionnyie-volnyi/
 

Для описания любого взаимодействия необходимо базовое волновое уравнение. В отличие от ОТО, это уравнение получается совершенно другим способом, стартуя из одного из фундаментальных законов сохранения в физике. Соответственно, и выводы получаются, в отличие от ОТО, естественными, а не фантастическими.

Здесь мы будем говорить о гравитации, онтология которой следует из физики, а не фантазий.